[054EN] A Thermodynamic and Aerodynamic Analysis of the Condensation Over Aeroplane Wings

Matthew Wang

In humid weather, it is not uncommon to see the peculiar view of the condensation of water over the wings of aeroplanes. The explanation of such a phenomenon can be found in numerous online forums and discussion groups. However, some of these explanations online are not correct, while most that the author has seen are qualitative. This article aims to analyse the phenomenon mathematically under a particular formulation, using thermodynamic and aerodynamic theories.

This article will start with a qualitative discussion of why such condensation can form. A hypothetical formulation will then be constructed, and the formation of such condensation explained mathematically. The validity of the assumptions made during the process will be analysed at the end.

Why water vapour condenses?

It is common sense that water vapour is present in the air that surrounds us. On a cold morning, the condensation of water vapour can be found in the form of fog. Fog is fundamentally the suspension of very small liquid water droplets in the air, and the condensation fog found over a wing is not different.

Water normally exists in everyday life in the form of liquid, then how come it can also exist in air in the form of vapour? The concept of partial pressure must first be introduced. Assume that there is 1% of water (by number of molecules, roughly 0.62% by “weight”) in atmospheric air (pressure p_{atm}=101.325\text{kPa}). The partial pressure of water in this case is p_w=0.01\times p_{atm}=1.01\text{kPa}. The reason why the partial pressure can be calculated in this way is related to the properties of an “ideal gas”, and it will not be explained in further detail here.

When pressure is lowered, the boiling point (known in thermodynamics as the “saturation temperature”) will decrease. This is why cooking is difficult at high altitudes. If the pressure is 1.01kPa, the saturation temperature is approximately 9℃. This is to say, under atmospheric pressure, when the temperature is above 9℃, 1% of water can happily exist in the air in the form of vapour, because the temperature is above the boiling point at its partial pressure (the water vapour is said to be “superheated”).

How can this water then condense? You may already have the answer, which is to lower the temperature. If you take some ice cream out of the fridge under this condition, you may very well observe some fog around it, which is a consequence of the water condensing in the air surrounding your ice cream, because the air in the immediate vicinity of the ice cream is cooled by it.

If air is accelerated without you adding heat into it (known in thermodynamics as an “adiabatic process”), its temperature decreases. This is the reason why condensation can occur over the upper surface of a wing. It does not occur below the lower surface, because there, air is not accelerated (and mostly decelerated instead). The acceleration of air also lowers its pressure, and vise versa for deceleration. This pressure difference is what keeps an aeroplane flying.

The whole picture is, unfortunately, more complicated. You may have already asked: “But if the pressure drops, certainly the saturation point drops with it, so who wins at the end of the day?” If you trust me, the answer is that the temperature drop dominates. If you are familiar with thermodynamics and compressible fluid mechanics, you can follow me into the subsequent sections where we shall dig deep into the equations to prove that this is indeed the case. If this is not your specialism, I hope the explanation above has already solved your confusion.

A hypothetical situation

Let us assume the following environmental conditions:

  • Atmospheric pressure p_{atm}=101.325\text{kPa}.
  • Atmospheric temperature T is 10℃, i.e. 283.15K.
  • The relative humidity of air is 95%. (The relative humidity is the ratio between the amount of water present, and the largest amount of water that can exist as vapour in that air i.e. right on the saturation point).
  • An aeroplane is taking off or landing at a true airspeed of 75m/s (approximately 150 knots).

How much temperature drop is needed?

At 10℃, the saturation pressure of water is 1.228kPa. Because the relative humidity is 95%, the partial pressure of water is 1.1666kPa. To saturate water vapour at this pressure, the temperature needed can be found as 9.23℃. This is to say, if pressure is held constant, a temperature drop of 0.77℃ is required for the water to condense.

\Delta(T-T_s)=0.77\text{K}

We have assumed here that condensation will occur when the temperature decreases to the saturation temperature, in practice, the temperature decrease needs to be slightly larger because a certain degree of “supercooling” is required for nucleation of water droplets to happen at a significant rate. We will not consider this complexity for the purpose of the discussion.

However, the pressure of the air over an aeroplane wing is lower than atmospheric, and the partial pressure of water will lower proportionally (note that it is the fractional content of water molecules in the air that is conserved). As the partial pressure is lowered, the saturation temperature also decreases. It is necessary to quantify this relationship for the analysis to progress further. The thermodynamic relationship that quantifies this process is the Clausius-Clapeyron Equation:

\frac{dT_s}{dp}=\frac{v_{fg}T_s}{h_{fg}}

We shall assume here that the departure from the original pressure is not excessively large so that the derivative can be approximated to be a ratio of the incremental amounts of Ts and p, and that the right hand side takes the value of the ambient conditions (where T_s=9.23℃, h_{fg}=2477.2kJ/kg, v_{fg}=106.318m3/kg). This ratio then evaluates to 0.0121.

\Delta T_s \approx 0.0121 \Delta p_w

Note that these approximations are necessary because v_{fg} and h_{fg} are not available in an analytical form (for water) for the equation to be integrated. Therefore, for a (water vapour partial) pressure decrease of one Pascal, which is equivalent to an air pressure decrease of 86.9 Pascals, the saturation temperature will decrease by approximately 0.0121℃. The temperature drop and pressure drop happens simultaneously over an aeroplane wing, which is the real complexity of the problem of interest.

Flow around the aeroplane

We first calculate the speed of sound and the aeroplane Mach number in this situation:

c=\sqrt{\gamma R T}=337.3\text{m/s}

M=\frac{v}{c}=0.222

Note that the Mach number is necessary for compressible flow calculations. It is usually said that air can be treated as incompressible (in a fluid mechanics sense) if the Mach number is less than 0.3, which is true. Under such conditions, the famous Bernoulli’s equation can be recovered from these equations, and the ideal gas Equation of State, p=\rho RT, can be used to explain the temperature drop associated with the pressure drop. However, the compressible theory is used here for generality.

We assume that the free stream has Mach number M, and at a location of interest (call it point A) over the wing, the Mach number increments into M_A=M+\Delta M. Also assume that the free stream and point A are connected by an adiabatic streamtube. This is to say, the flow is sufficiently fast that the heat transfer to and from the surrounding air is negligible. If the heat transfer in the air is so rapid that the temperature is always uniform, the phenomenon of interest cannot be observed.

By some relationships in compressible fluid mechanics (we are assuming isentropic expansion here, to which being adiabatic is a prerequisite):

\frac{T_0}{T}=1+\frac{\gamma-1}{2}M^2

\frac{p_0}{p}=(\frac{T_0}{T})^{\frac{\gamma}{\gamma-1}}

We find that the stagnation temperature T_0 is 285.94K, and the stagnation pressure p_0 is 104.864kPa. We have gone from the free stream condition to the stagnation condition, which is what links the condition at point A to the free stream condition. We shall now go from here to the condition at point A. To do this we make the same assumption as we had in the thermodynamic analysis, which is that the conditions at point A is not significantly different from the ambient conditions so that we can approximate incremental differences (to a first-order accuracy) by differentials. Because we have already constrained a small difference before, making this approximation again greatly simplifies the calculations.

Differentiating the above equations, we get (at point A):

\Delta T \approx dT = -T_0(\gamma-1)(1+\frac{\gamma-1}{2}M^2)^{-2}MdM

\Delta p \approx dp = -p_0(\frac{\gamma}{\gamma-1})(1+\frac{\gamma-1}{2}M^2)^{\frac{1-2\gamma}{\gamma-1}}(\gamma-1)MdM

where dM \approx \Delta M. These values evaluate to:

\Delta T \approx -24.90 \Delta M

\Delta p \approx -31184.47 \Delta M

In terms of the partial pressure of water:

\Delta p_w = 0.0115 \Delta p \approx -359.04 \Delta M

From the thermodynamic analysis, we have:

\Delta T_s \approx 0.0121 \Delta p_w = -4.34 \Delta M

Therefore:

\Delta (T-T_s)=\Delta T - \Delta T_s \approx -20.56 \Delta M

In the thermodynamic analysis, we have concluded that \Delta (T-T_s) needs to be 0.77K for condensation to happen. Therefore:

\Delta M =0.037

We note that \Delta M=0.167M. Because the incremental amount differs from the absolute amount by an order-of-magnitude, the first-order approximations we have made can be concluded as (roughly) correct.

But…is this feasible?

Substituting this \Delta M back to the equations above, we find that the pressure at point A needs to decrease by 1.168kPa. In terms of the pressure coefficient, this evaluates to:

c_p=-0.34

Now the question becomes, can we obtain c_p=-0.34 above the wing of an aeroplane? The answer is easily. The following plot is extracted from NACA Report No. 465, and it shows the theoretical pressure distribution over a NACA-2412 aerofoil. It is evident that, starting from several degrees of angle-of-attack, c_p < -0.34 extends from the leading edge to at least 70% chord on the upper surface.

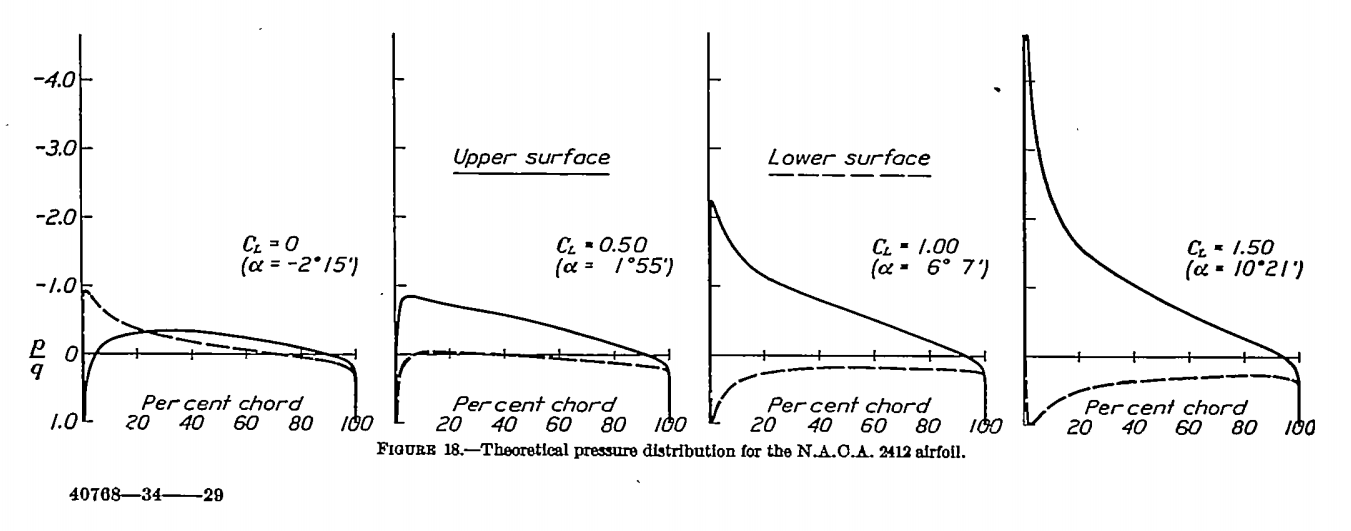
Fig. 1 Theoretical pressure distribution for the NACA 2412 aerofoil

Therefore, we have demonstrated theoretically and mathematically how such condensation over aeroplane wings can happen.

How trustworthy are the “small difference” approximations?

It is questionable how valid are the small difference approximations we have made before, because we have concluded that the difference is almost one fifth of the original amount. Luckily, the functions of temperature and pressure in terms of the Mach number are convex functions well up to M=0.5. That is to say, if \Delta M is not small, then the temperature and pressure drops will be more than we have approximated. In terms of the effect on the final result, the temperature drop outweighs the pressure drop (really the saturation temperature drop associated with it) by as much as six times. As a consequence, the phenomenon can only be more pronounced than what our model predicts.

High G manoeuvres

Following the analysis above, let us assume that, under a particular environmental condition, there is a critical pressure coefficient, the exceeding of which will lead to condensation around an aeroplane. This explains why condensation clouds can form suddenly when a fighter jet makes manoeuvres, as illustrated by the following photograph.

Fig. 2 A jet fighter in a high G manoeuvre, with condensation clouds forming over the wings

When this jet fighter manoeuvres, the lift force required from the wings is larger than what is normally needed when flying straight and level, and the excess amount of force accelerates the aeroplane. In order to generate this larger lift, the pressure must become lower on the upper surface and higher on the lower surface. This is completed by increasing the angle-of-attack, and the process is illustrated as going from left to right on Fig. 1.

As this happens, the pressure coefficient over the upper surface of the wing can decrease to a value below the critical value, so the condensation appears. If the pressure coefficient decreases further, the condensation cloud can become larger.

Acknowledgements

The author wishes to address special thanks to Mr Issac Dai, a natural scientist of Cambridge University and an aviation photographer, for kindly offering the very nice illustrations of the phenomenon concerned.

Leave a Reply